P3379 【模板】最近公共祖先（LCA）(st表，tarjan两种版本)

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 $N,M,S$，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 $N-1$ 行每行包含两个正整数 $x,y$，表示 $x$ 结点和 $y$ 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 $M$ 行每行包含两个正整数 $a,b$，表示询问 $a$ 结点和 $b$ 结点的最近公共祖先。

输出格式

输出包含 $M$ 行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例 #1

输入 #1

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

输出 #1

4
4
1
4
4

说明/提示

对于 $30\%$ 的数据，$N\le 10$，$M\le 10$。

对于 $70\%$ 的数据，$N\le 10000$，$M\le 10000$。

对于 $100\%$ 的数据，$1\le N,M\le 5\times 10^5$，$1\le x,y,a,b\le N$，不保证 $a\ne b$。

样例说明：

该树结构如下：

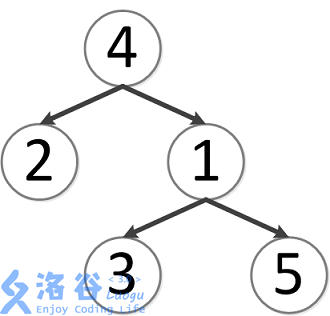
第一次询问：$2,4$ 的最近公共祖先，故为 $4$。

第二次询问：$3,2$ 的最近公共祖先，故为 $4$。

第三次询问：$3,5$ 的最近公共祖先，故为 $1$。

第四次询问：$1,2$ 的最近公共祖先，故为 $4$。

第五次询问：$4,5$ 的最近公共祖先，故为 $4$。

故输出依次为 $4,4,1,4,4$。

2021/10/4 数据更新 @fstqwq：应要求加了两组数据卡掉了暴力跳。

题解

递归版

#include <bits/stdc++.h>
using namespace std;
const int N=6e5+10;
typedef long long ll;
int n,m,s;
vector<int>e[N];
int st[N][20];
int pw;
int deep[N];
bool vis[N];
void dfs(int u,int f)
{deep[u]=deep[f]+1;st[u][0]=f;vis[u]=true;// cout<<u<<' '<<f<<endl;for(int p=1;p<=pw;p++){st[u][p]=st[st[u][p-1]][p-1];}for(auto v:e[u]){if(vis[v])continue;dfs(v,u);}
}int lca(int a,int b)
{if(deep[a]<deep[b]){swap(a,b);}for(int p=pw;p>=0;p--){if(deep[st[a][p]]>=deep[b])a=st[a][p];}if(a==b)return a;for(int p=pw;p>=0;p--){if(st[a][p]!=st[b][p]){a = st[a][p];b = st[b][p];}}// cout<<st[a][0]<<endl;return st[a][0];
}void solve()
{cin>>n>>m>>s;for(int i=1;i<=n-1;i++){int u,v;cin>>u>>v;e[u].push_back(v);e[v].push_back(u);}int a,b;pw = log2(n);dfs(s,0);for(int i=1;i<=m;i++){cin>>a>>b;cout<<lca(a,b)<<endl;}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;// cin>>t;while(t--){solve();}return 0;
}

tarjan算法模板

#include <bits/stdc++.h>
using namespace std;
const int N=6e5+10;
typedef long long ll;
int n,m,s;
vector<int>e[N];
vector<pair<int,int>>q[N];
int fa[N];
int ans[N];
bool vis[N];
int find(int i)
{return fa[i]==i?i:fa[i]=find(fa[i]);
}void tarjan(int u,int f)
{vis[u]=true;fa[u]=u;for(auto v:e[u]){if(v==f)continue;tarjan(v,u);fa[v]=u;}for(auto nd:q[u]){int v = nd.first;int id = nd.second;if(vis[v]){ans[id]=find(v);}}
}void solve()
{cin>>n>>m>>s;for(int i=1;i<=n-1;i++){int u,v;cin>>u>>v;e[u].push_back(v);e[v].push_back(u);}for(int i=1;i<=m;i++){int u,v;cin>>u>>v;q[u].push_back({v,i});q[v].push_back({u,i});}for(int i=1;i<=n;i++)fa[i]=i;tarjan(s,0);for(int i=1;i<=m;i++)cout<<ans[i]<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;// cin>>t;while(t--){solve();}return 0;
}