当前位置：首页 > news >正文

webgl 变换矩阵：旋转、平移、缩放

news 2025/11/1 9:51:36

一，变换矩阵

对于简单的变换可以使用数学表达式来实现，但是当情形逐渐变得复杂时，利用表达式运算就会变得相当繁琐。好在我们可以使用另一个数学工具 -------- 变换矩阵 。变换矩阵在三维计算机图形学运用的非常广泛，以至于着色器本身就实现了矩阵和矢量相乘的功能。

二，变换矩阵：旋转矩阵

1，推导变换矩阵

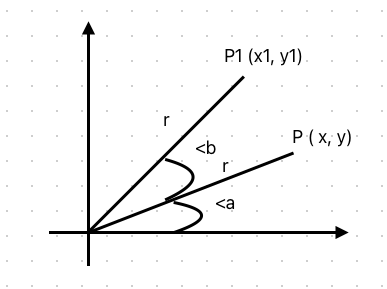
由 P (x,y) 逆时针旋转 b 度获得 P1(x1,y1); 由三角函数可以获得 P 点和 P1 点坐标之间的关系

$x1 = x*cosb - ysinb$

$y1 = x*sinb + ycosb$

$z1 = z$

$w1 = w;$

根据矩阵的乘法

$\begin{bmatrix} x1\\ y1\\ z1\\ w1 \end{bmatrix} = \begin{bmatrix} a & q & c&d \\ e& f& g&h \\ i& j& k&l \\ m& n& o& p \end{bmatrix} * \begin{bmatrix} x\\ y\\ z\\ w \end{bmatrix}$

可以得到

$x1 = ax+qy+cz+dw$

$y1 = ex+fy+gz+hw$

$z1=ix+jh+kz+lw$

$w1=mx+ny+oz+pw$

对比上面的三角函数表达式和下方的矩阵乘法

$a=cosb , q = -sinb, c=0, d=0$

$e=sinb, f=cosb, g=0, h=0$

$i=0, j=0, k=1, l=0$

$m=0, n=0, o=0, p=1$

所以，获得的旋转矩阵为 $\begin{bmatrix} cosb &-sinb &0 &0 \\ sinb& cosb& 0&0 \\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$

2，修改顶点着色器编码

使用 mat4 声明 4 维矩阵变量

// 顶点着色器, 通过矩阵乘法实现平移
const VSHADER_SOURCE = `
attribute vec4 a_Position;
uniform mat4 u_xformMatrix;void main() {gl_Position = u_xformMatrix * a_Position;}
`;

3，创建变换矩阵

webgl 中创建矩阵是 按列主序。

 // 创建平移矩阵const xformMatrix = new Float32Array([cosB, sinB, 0.0, 0.0, -sinB, cosB, 0.0, 0.0,0.0, 0.0, 1.0, 0.0,0.0, 0.0, 0.0, 1.0,])

4，传递变量绘制三角形

 // 获取 u_xformmatrix 变量的存储位置const u_xformMatrix = state.gl.getUniformLocation(state.gl.program, 'u_xformMatrix') as WebGLUniformLocation;state.gl?.uniformMatrix4fv(u_xformMatrix, false, xformMatrix);// 绘制三角形//  state.gl.drawArrays(state.gl.TRIANGLE_STRIP, 0, n);state.gl.drawArrays(state.gl.TRIANGLES, 0, 3);

二。变换矩阵：平移矩阵

1，推导平移矩阵

假设点P（x,y,z,1)，经过平移得到 P1(x1,y1,z1,1)

$x1 = x+Tx ; y1 = y+Ty; z1 = z+Tz;$

由矩阵的乘法可得

$\begin{bmatrix} x1\\ y1\\ z1\\ 1 \end{bmatrix} = \begin{bmatrix} a & b & c&d \\ e& f& g&h \\ i& j& k&l \\ m& n& o& p \end{bmatrix} * \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

可以得到

$x1 = ax+by+cz+dw$

$y1 = ex+fy+gz+hw$

$z1=ix+jh+kz+lw$

$w1=mx+ny+oz+pw$

可以得到

$a=1; b=0; c=0, d=Tx$

$c=0; f=1; g=0; h=Ty;$

$i=0;j=0;k=1; l=Tz;$

$m=0; n=0; o=0; p=1;$

从而可以得到平移矩阵` $\begin{bmatrix} 1 &0 &0 &Tx \\ 0& 1& 0&Ty \\ 0& 0& 1& Tz\\ 0& 0& 0& 1 \end{bmatrix}$ ，其中 $Tx, Ty, Tz$ 分别为x, y, z 轴的平移分量。

2，创建平移矩阵

假设使三角形水平向右移动 0.5，则 $Tx=0.5;Ty=0; Tz=0;$

webgl 中创建矩阵是按列主序

// 创建平移矩阵const xformMatrix = new Float32Array([1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0,0.0, 0.0, 1.0, 0.0,0.5, 0.0, 0.0, 1.0,])

3, 传递变量绘制三角形

 // 获取 u_xformmatrix 变量的存储位置const u_xformMatrix = state.gl.getUniformLocation(state.gl.program, 'u_xformMatrix') as WebGLUniformLocation;state.gl?.uniformMatrix4fv(u_xformMatrix, false, xformMatrix);// 绘制三角形//  state.gl.drawArrays(state.gl.TRIANGLE_STRIP, 0, n);state.gl.drawArrays(state.gl.TRIANGLES, 0, 3);

三，变换矩阵：缩放矩阵

1，推导缩放矩阵

假设 $Sx,Sy,Sz$ 分别为 x, y, z 轴上的缩放因子，则可得

$x1 = Sx*x; y1 = Sy*y, z1 = Sz*z$

将上式同第二步的矩阵乘法等式做比较，可得缩放矩阵

$\begin{bmatrix} x1\\ y1\\ z1\\ 1 \end{bmatrix} = \begin{bmatrix} Sx & 0 & 0&0 \\ 0& Sy& 0&0 \\ 0& 0& Sz&0 \\ 0& 0& 0& 1 \end{bmatrix} * \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

2，创建缩放矩阵

假设三角形沿 y 轴缩小0.5 倍，则 $Sx = 1.0; Sy = 0.5; Sz = 1.0;$

 // 创建平移矩阵const xformMatrix = new Float32Array([1.0, 0.0, 0.0, 0.0, 0.0, 0.5, 0.0, 0.0,0.0, 0.0, 1.0, 0.0,0.0, 0.0, 0.0, 1.0,])

3，传递参数，绘制三角形。

可以看到三角形沿 y 轴缩小了一半。

 // 获取 u_xformmatrix 变量的存储位置const u_xformMatrix = state.gl.getUniformLocation(state.gl.program, 'u_xformMatrix') as WebGLUniformLocation;state.gl?.uniformMatrix4fv(u_xformMatrix, false, xformMatrix);// 绘制三角形//  state.gl.drawArrays(state.gl.TRIANGLE_STRIP, 0, n);state.gl.drawArrays(state.gl.TRIANGLES, 0, 3);

查看全文

http://www.dtcms.com/a/553507.html