当前位置：首页 > news >正文

【深度学习笔记 Ⅱ】5 梯度消失和梯度爆炸

news 2025/7/20 7:16:53

在深度学习中，**梯度消失（Vanishing Gradients）和梯度爆炸（Exploding Gradients）**是训练深层神经网络时的两大常见问题，它们与反向传播中的梯度计算直接相关。以下是详细解析：

1. 梯度消失与梯度爆炸的定义

(1) 梯度消失

现象：在反向传播过程中，梯度逐层指数级减小，导致浅层网络的权重几乎不更新。
后果：浅层网络无法有效学习，模型仅依赖深层特征，性能下降。

(2) 梯度爆炸

现象：梯度逐层指数级增大，最终超过数值表示范围（如NaN）。
后果：权重更新过大，模型无法收敛，甚至引发数值溢出。

2. 原因分析

(1) 数学根源

反向传播通过链式法则计算梯度。假设网络有 (L) 层，每层的梯度计算为：
在这里插入图片描述

(2) 典型诱因

因素	梯度消失	梯度爆炸
激活函数	Sigmoid、Tanh（导数<1）	ReLU（无上界）
权重初始化	过小（如N(0, 0.01)）	过大（如N(0, 1)）
网络深度	深层网络更易发生	深层网络更易发生
优化器	学习率过小可能加剧	学习率过大直接引发

3. 解决方案

(1) 梯度消失的缓解方法

使用合适的激活函数：
- ReLU 及其变种（LeakyReLU、PReLU、Swish）：导数在正区间为1，避免连乘衰减。
- 避免Sigmoid/Tanh（尤其深层网络）。
权重初始化：
残差连接（ResNet）：
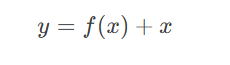
- 通过跳跃连接（Skip Connection）绕过部分层，梯度可直接回传。
Batch Normalization：
- 保持每层输入的分布稳定，缓解梯度幅度波动。

(2) 梯度爆炸的缓解方法

梯度裁剪（Gradient Clipping）：
- 设定阈值，强制梯度不超过该值。
```
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
```
权重正则化：
- L2正则化惩罚大权重，限制梯度幅度。
降低学习率：
- 避免单步更新过大。

(3) 通用策略

使用LSTM/GRU（RNN中）：
- 门控机制控制梯度流动，缓解时序上的梯度问题。

监控梯度：

打印各层梯度范数，早期发现问题。

for name, param in model.named_parameters():if param.grad is not None:print(f"{name}: {param.grad.norm()}")

4. 代码示例

(1) 梯度裁剪（PyTorch）

optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
for epoch in range(epochs):optimizer.zero_grad()outputs = model(inputs)loss = criterion(outputs, labels)loss.backward()# 梯度裁剪（阈值=1.0）torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)optimizer.step()

(2) 权重初始化（ReLU网络）

import torch.nn as nndef init_weights(m):if isinstance(m, nn.Linear):nn.init.kaiming_normal_(m.weight, mode='fan_in', nonlinearity='relu')m.bias.data.fill_(0.01)model.apply(init_weights)

5. 现象对比

特征	梯度消失	梯度爆炸
梯度表现	趋近于0	数值溢出（NaN/Inf）
训练现象	浅层权重几乎不变	损失剧烈震荡或突变为NaN
典型激活函数	Sigmoid、Tanh	ReLU（无上界）
解决方案	ReLU、残差连接、BN	梯度裁剪、权重初始化