java数据类型

在计算机中是如何存储数据的？
请看下面的 java 代码：

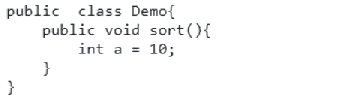
在C语言当中所有的变量都叫做指针，a 作为一个指针指向当前这个它是要存储当前实际数据的地址。假设当前我们给10开辟好内存空间，对它进行存储，那么 a 记录着10的地址 0xbc 内存空间。

八种基本数据类型

java是一种强类型的语言，这就意味着每一种变量都有一种类型。在java中一共有8种基本数据类型和三种引用数据类型。
数据类型的作用：表示数据在内存中的存储形式

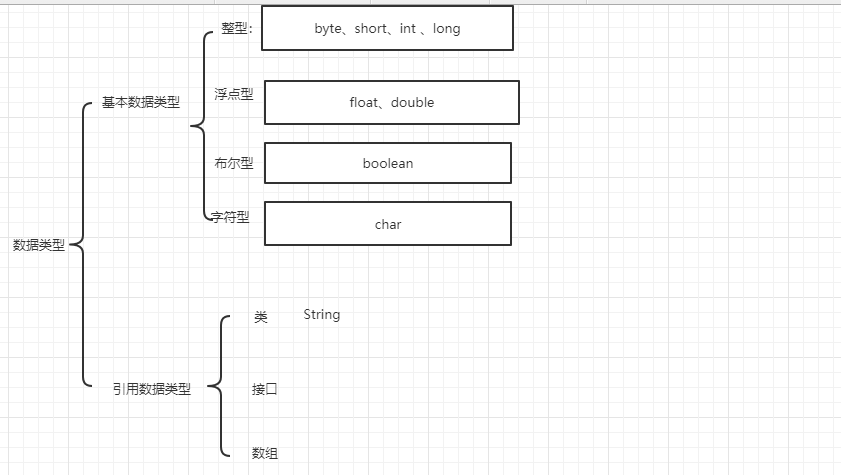
下面主要讲解基本数据类型

存储需求以及取值范围

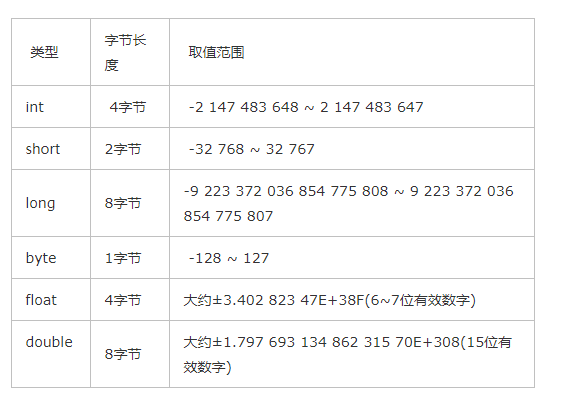
（注意这里 int 类型刚好超过20亿）

字节(B)是计算机信息技术用于计量存储容量和传输容量的一种计量单位，1个字节等于8位二进制，即1Byte（字节）= 8bit(位)

原码反码和补码

计算机中对数据的二进制存储形式 ------- 补码
下面讨论的皆为byte类型

原码：45:00101101， -45:10101101
在最高位代表符号位区分正数还是负数，0代表正数，1代表负数

反码：45:00101101， -45:11010010
正数的原码和反码相同，负数的反码等于原码的符号位不变，其余各位按位取反

补码：45:00101101， -45:11010011
正数的原码反码和补码都形同，负数的补码等于在其反码基础上末尾+1

为什么计算机设计反码和补码？

计算机只有加法没有减法，在做减法运算的时候，可以认为是加上一个负数，这样可以减少计算机电路的复杂度。
使用原码进行减法运算会出现问题，例如计算1-1，因为计算机有加法没有减法，所以计算机自动换算成1+(-1)
1-1=1+(-1)=[00000001]原+[10000001]原=[10000010]原=-2 （符号位也参与运算）与结果不符
1-1=1+(-1)=[00000001]原+[10000001]原=[00000001]反+[11111110]反=[11111111]反=[10000000]原=-0
通过反码计算的结果是11111111在计算一次反就成原码了，得出的结果是正确的，但是有一个问题是 00000000可以代表+0 10000000可以代表-0，其实是一样的，用2个编码实在是浪费。于是出现了补码解决0的符号以及两个编码的问题
1-1=1+(-1)=[00000001]原+[10000001]原=[00000001]补+[11111111]补=[00000000]补=[00000000]原
这样0用[00000000]表示，而以前出现问题的-0则不存在了。

总结：反码是为了解决减法运算，补码是为了解决反码产生的±0的问题

为什么byte类型127+1是-128

先看下图

使用补码不仅仅修复了0的符号以及存在两个编码的问题，而且还能够多表示一个最低数，这就是为什么8位二进制使用原码或反码表示的范围为[-127, +127]，而使用补码表示的范围为[-128, 127]的原因。
因为机器使用补码，所以对于编程中常用到的32位int类型，可以表示范围是: [-2^31, 2^31-1] 因为第一位表示的是符号位，而使用补码表示时又可以多保存一个最小值。

浮点类型

浮点类型在计算机当中的存储

首先我们来看一下浮点类型在我们的计算机当中是如何存储的

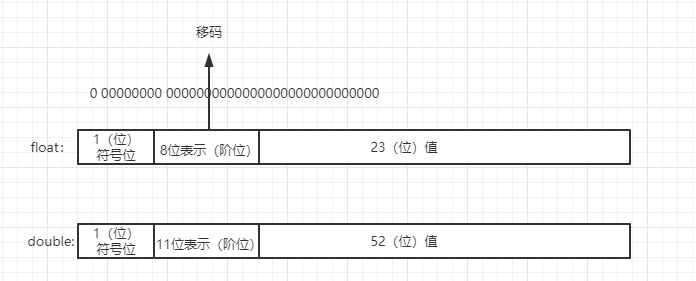
float存储需求是4字节（32位）, 其中1位最高位是符号位，中间8位表示阶位，后32位表示值
double存储需求是8字节（64为）,其中1位最高位是符号位，中间11位表示阶位，后52位表示值

double表示这种类型的数值精度是float类型的两倍（有人称之为双精度数值)。绝大部分应用程序都采用double类型。在很多情况下，float类型的精度很难满足需求。例如，用7位有效数字足以精确地表示普通雇员的年薪，但表示公司总裁的年薪可能就不够用了。实际上，只有很少的情况适合使用float类型，例如，需要快速地处理单精度数据，或者需要存储大量数据。

浮点类型的精度丢失

1. 产生精度丢失的原因

首先我们看一个例子

public class SimpleTest {public static void main(String[] args) {System.out.println(1.2 - 1);}
}

输出：

0.19999999999999996

这和我们预期的情况完全不符

我们来将10进制的0.2转化为2进制进行存储，算法是乘以2直到没有了小数为止

0.2 * 2 = 0.4 —— 取整数部分 0
0.4 * 2 = 0.8 —— 取整数部分 0
0.8 * 2 = 1.6 —— 取整数部分 1
0.2 * 2 = 0.4 —— 取整数部分 0
。。。。。。

0.2的2进制从上到下可以表示为 00110011…

注意：上面的计算过程循环了，也就是说*2永远不可能消灭小数部分，这样算法将无限下去。很显然，小数的二进制表示有时是不可能精确的 。其实道理很简单，十进制系统中能不能准确表示出1/3呢？同样二进制系统也无法准确表示1/10。这也就解释了为什么浮点型减法出现了"减不尽"的精度丢失问题。

还有更多请看：
https://www.cnblogs.com/straybirds/p/6295036.html?utm_source=itdadao&utm_medium=referral

精度丢失就是我们的位数不够表示我们整个数值了

2. 如何解决精度丢失

浮点数值不适用于禁止出现舍入误差的金融计算中。例如，命令System.out.println(2.0-1.1)将打印出0.8999999999999999，而不是人们想象的0.9。其主要原因是浮点数值采用二进制系统表示，而在二进制系统中无法精确的表示分数1/10。如果需要在数值计算中不含有任何舍入误差，就应该使用 BigDecimal 类。

public static void main(String[] args) {BigDecimal b1 = new BigDecimal(Float.toString(1.2f));BigDecimal b2 = new BigDecimal(Float.toString(1));float s = b1.subtract(b2).floatValue(); System.out.println("s----" + s);
}

BigDecimal 将数值转换成字符串，通过字符串的加减法，最终得到想要的数值。

char类型

1. java字符类型采用Unicode字符集编码，Unicode是世界通用的定字长字符集，所用字符都是16位。字符类型实际上是一个16位无符号整数，这个数对应字符的编码

public static void main(String[] args) {char c1 = '中';char c2 = '\u4e2d';System.out.println(c1);System.out.println(c2);
}

注释：’4e2d‘为’中‘所对应的16位Unicode编码

char 类型可以直接转成 int 类型，所以 char c1 = ‘中’ 不报错
若浮点类型不能精确计算就用 BigDecimal 类

2. 任何一个字符都可以转化为一个整数，整数的范围是 0-65535

public static void main(String[] args) {int  a = '中';System.out.println(a);
}

4. 可以查看某个数对应着那个字符
   Java 中的 char 类型是 16位无符号整数，本质存储的是字符的 Unicode 码点（数字形式），当给 char 变量赋整数值时，Java 会自动将其解释为对应的 Unicode 字符

本质是将 Unicode 码点 69 存入变量，而码点 69 在字符集中对应字母 E，因此输出结果为 E。这是 Java 基于 Unicode 编码的隐式转换特性。

public static void main(String[] args) {char c = 69;System.out.println(c);}

输出：

E

System.out.println((int)c)）才会输出数字 69

5. 转义字符
   对于不方便输出的字符可以采用转义字符表示

例如：

public static void main(String[] args) {int num = 100;String json = "{"+"\"count\":"+num+"}";// /斜杠 \反斜杠String dataString = "[{\"id\":\"1\" ,\"name\":\"张三\"},{\"id\":\"2\" ,\"name\":\"李四\"},{\"id\":\"3\" ,\"name\":\"王五\"}]";System.out.println(json);
}

输出：

{“count”:100}

转义字符	含义：
\n	表示回车
\r	表示换行符
\\	表示反斜杠( \ )
\'	表示单引号( ’ )
\"	表示双引号( " )

boolean类型

boolean（布尔）类型有两个值：flase 和 true，用来判断逻辑条件。
注意数值型和 boolean 之间不能直接转化。

强制类型转换

图中所标均为合法转换，实线箭头均为无信息丢失的转换，虚线箭头表示可能有精度丢失的转换

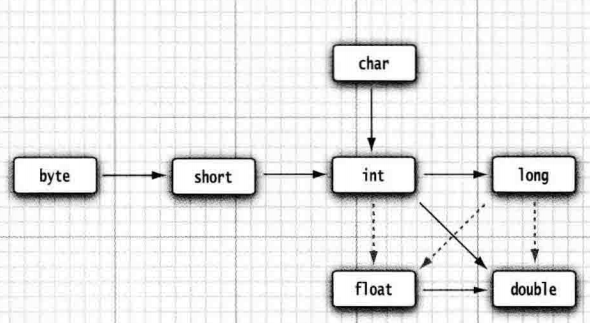
图中没标的转换形式需要经过强制类型转换才能做到，但是强制类型转换一定会造成精度丢失

我们来看以下代码：

public static void main(String[] args) {byte a = 127;byte b = (byte)(a+1);System.out.println(b);   
}

127+1=[01111111]补+[00000001]补=[10000000]补=-128(补)

若写成

byte b = a+1;

这里会报错，因为 a+1 存储的是 int 类型的数据，这是因为 a+1 其中 1 默认是 int 类型的数据，byte+int 结果是一个 int 类型的数据。

若这样写

byte c = 127; byte b = a+c;

这里也会报错，所得出的值其实也是一个 int 类型数据，java 当中存储数据存储整型的数据默认是用 int 去存储的，需要强制类型转换。

也可以这样修改：

byte c = 127; int b = a+c;

运算

运算符：

按位亦或操作

相当于加法，相同为0，不同为1：

例题：有一个非空整数数组 nums，除了某个元素只出现一次以外，其余每个元素均出现两次，找出那个只出现了一次的元素。注意需要设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

我们可以使用 异或运算 来解决该问题
假设数组中有 2m+1 个数，其中有 m 个数各出现两次，一个数出现一次，数组中的全部元素的异或运算结果总是可以写成如下形式：
(a1 ⊕ a1) ⊕ (a2 ⊕ a2) ⊕ ⋯ ⊕ (am ⊕ am) ⊕ am+1
上式可化简和计算得到如下结果：
0 ⊕ 0 ⊕ ⋯ ⊕ 0 ⊕ am+1 = am+1
因此，数组中的全部元素的异或运算结果即为数组中只出现一次的数字

public int singleNumber(int[] nums) {int single = 0;for(int i=0;i<nums.length;i++){single ^= nums[i];}return single;
}

移位运算

1. 左移(<<)：右边空出来的位用 0 填补高位左移溢出则舍弃该高位
   左移几位其实就是这个数“2“的几次幂 —> 乘法
2. 有符号右移(>>)：左边空出来的位用 0 或 1 填补，正数用 0 负数用 1 填补。
   右移几位其实就是这个数/2的几次幂 —> 除法
3. 无符号右移(>>>)：数据进行右移时，高位出现的空位，无论原高位是什么，空位都用 0 补
   注意：整型默认是使用int，所以计算无符号右移时，是按照32位二进制数进行计算的

移位运算与乘法运算的时间比较：

public static void main(String[] args) {long startTime=System.nanoTime();//获取开始时间System.out.println(2*16);long endTime=System.nanoTime();//获取结束时间System.out.println("程序运行时间:"+(endTime-startTime)+"ns");long startTime1=System.nanoTime();System.out.println(2<<4);long endTime1=System.nanoTime();System.out.println("程序运行时间:"+(endTime1-startTime1)+"ns");}

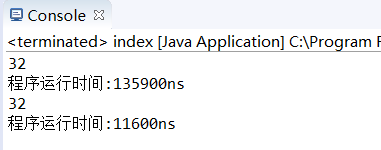
同样计算 2*16，移位运算与乘法运算的时间相差很大，所以有时候乘法运算使用移位运算效率会更高