比较含距离和顺序的结构相似性

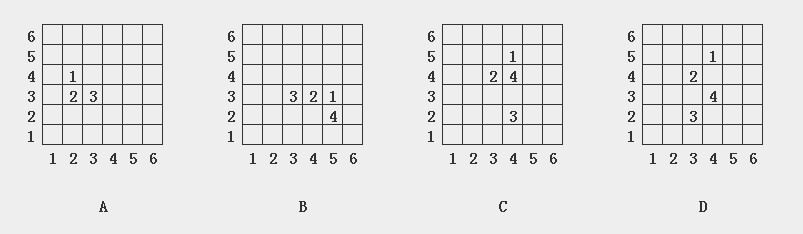
在平面上有4个结构A，B，C，D，这4个结构有位置，并且有顺序，比较A和B，C，D哪个更像？

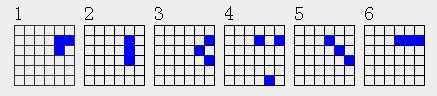
A就是3a1

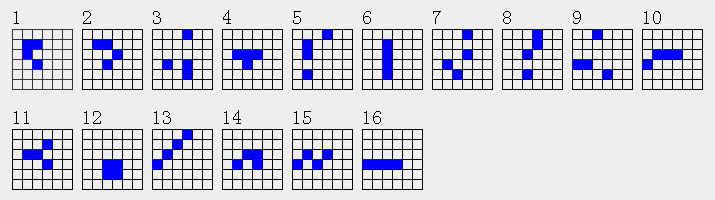
B是4a4，C是4a3，D是4a8.

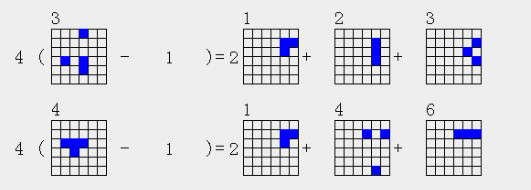
4(4a3-1)=2*3a1+3a2+3a3

4(4a4-1)=2*3a1+3a4+3a6

因为4a3，4a4减一都可得到3a1，

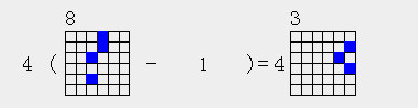
4(4a8-1)=4*3a3

但4a8减1只能得到3a3

因此有理由认为4a3和4a4与3a1在结构上要更相似些。

用结构加法去计算

13(3a1+1)=2*4a1+4a2+2*4a3+2*4a4+4*4a12+2*4a14

6(3a2+1)=4a3+4a5+4*4a6

15(3a3+1)=2*4a1+4a2+4a3+3*4a5+2*4a7+4*4a8+2*4a11

15(3a4+1)=4a2+4a4+2*4a9+3*4a10+2*4a11+2*4a14+4*4a15

9(3a5+1)=4a2+2*4a7+2*4a9+4*4a13

6(3a6+1)=4a4+4a10+4*4a16

代入4a3， 为0，0，1，0，0，0，0，0，0，0，0，0，0，0，0，0用同样的办法代入4a4，

0，0，0，1，0，0，0，0，0，0，0，0，0，0，0，0和4a8，0，0，0，0，0，0，0，1，0，0，0，0，0，0，0，0得到

4a4			4a3			4a8
0.1538	0		0.1538	0		0	0
0	1		0.1667	1		0	1
0	2		0.0667	2		0.267	2
0.0667	3		0	3		0	3
0	4		0	4		0	4
0.1667	5		0	5		0	5

设这种结构相似性的距离用1/3a1得到，则4a4和4a3的距离都是1/0.1538，而4a8是无穷大。

再比较距离的相似性，4a4-1可以得到3a1和3a2，3a3这里设3a2和3a3对结果没有影响，只考虑3a1，有两种可能

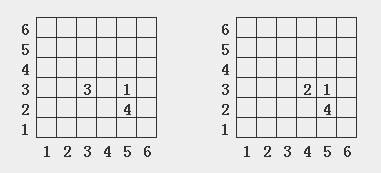
计算A到这两个结构的距离

x1	y1		x2	y2		(x2-x1)^2	(y2-y1)^2		根号		和	平均
2	4		5	3		9	1		3.1623		6.398	2.133
2	3		3	3		1	0		1
3	3		5	2		4	1		2.2361
x1	y1		x2	y2		(x2-x1)^2	(y2-y1)^2		根号		和	平均
2	4		5	3		9	1		3.1623		7.398	2.466
2	3		4	3		4	0		2
3	3		5	2		4	1		2.2361

平均为2.299

同样的方法计算4a3

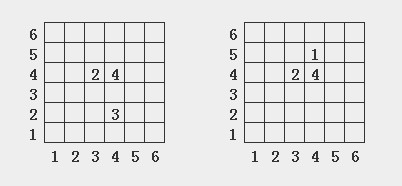
x1	y1		x2	y2		(x2-x1)^2	(y2-y1)^2		根号		和	平均
2	4		3	4		1	0		1		4.65	1.55
2	3		4	2		4	1		2.2361
3	3		4	4		1	1		1.4142
x1	y1		x2	y2		(x2-x1)^2	(y2-y1)^2		根号		和	平均
2	4		4	5		4	1		2.2361		5.064	1.688
2	3		3	4		1	1		1.4142
3	3		4	4		1	1		1.4142

距离平均为1.619

综合得到

	结构	距离		和
B	6.502	2.299		8.8
C	6.502	1.619		8.1
D	∞			∞

因此有理由猜测A和C更像。