二叉搜索树：高效的查找结构

二叉搜索树：高效的查找结构

大家好！今天我们来聊聊数据结构中的一位"明星选手"——二叉搜索树（Binary Search Tree，简称BST）。想象一下你在图书馆找书的情景：如果书籍是随机摆放的，你需要一本本翻看才能找到目标；但如果书籍是按照字母顺序排列的，你就可以像查字典一样快速定位。二叉搜索树就是这样一个让数据"有序"存储的结构，它能让我们在数据海洋中快速找到想要的信息。

一、二叉搜索树的基本概念

理解了二叉搜索树的比喻后，我们来看看它的正式定义。二叉搜索树是一种特殊的二叉树，它满足以下性质：

1. 每个节点都有一个键（key）和最多两个子节点（左子节点和右子节点）
2. 左子树中所有节点的键值小于当前节点的键值
3. 右子树中所有节点的键值大于当前节点的键值
4. 没有键值相等的节点（或者根据实现可以允许）

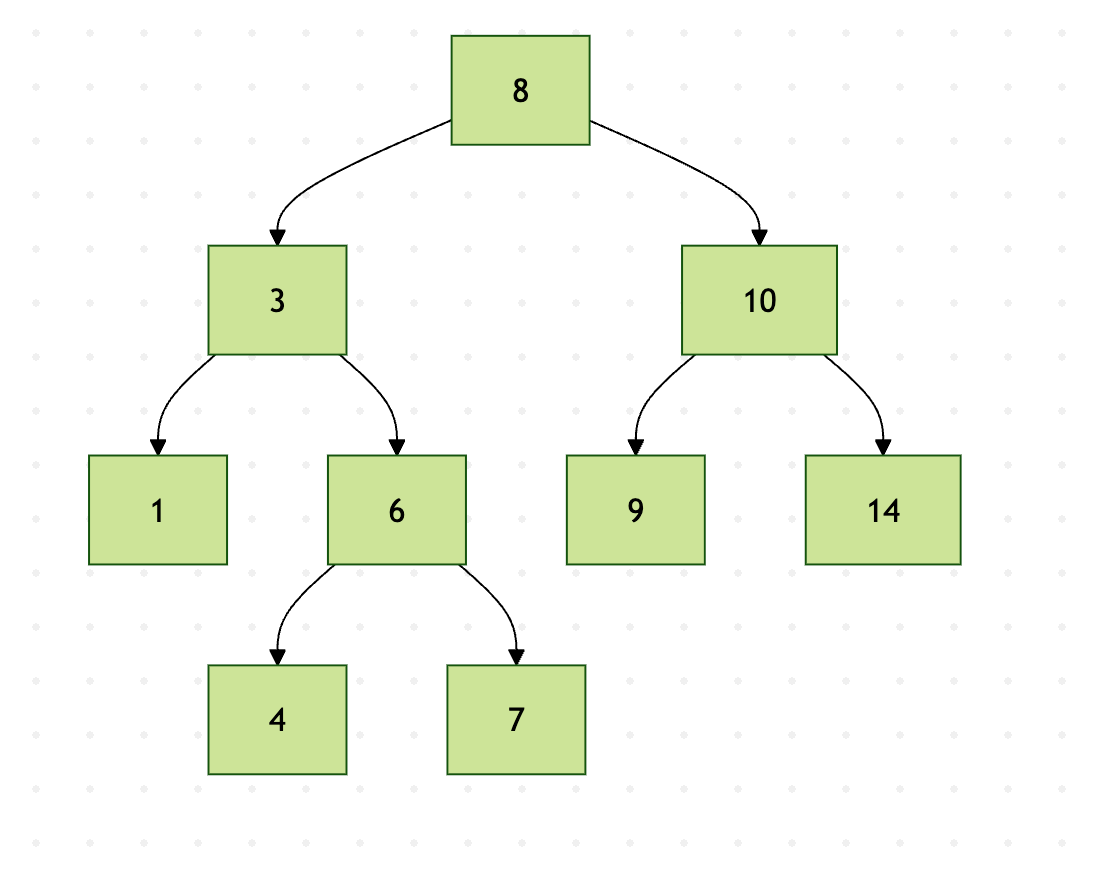
这是一个典型的二叉搜索树示例。可以看到，每个节点的左子树值都小于它，右子树值都大于它。

二、二叉搜索树的操作

让我们一起来看看二叉搜索树的核心操作：查找、插入和删除。这些操作都充分利用了BST的有序特性。

1. 查找操作

查找是BST最基础的操作，其时间复杂度在理想情况下是O(log n)。查找过程就像在做一个二分查找：

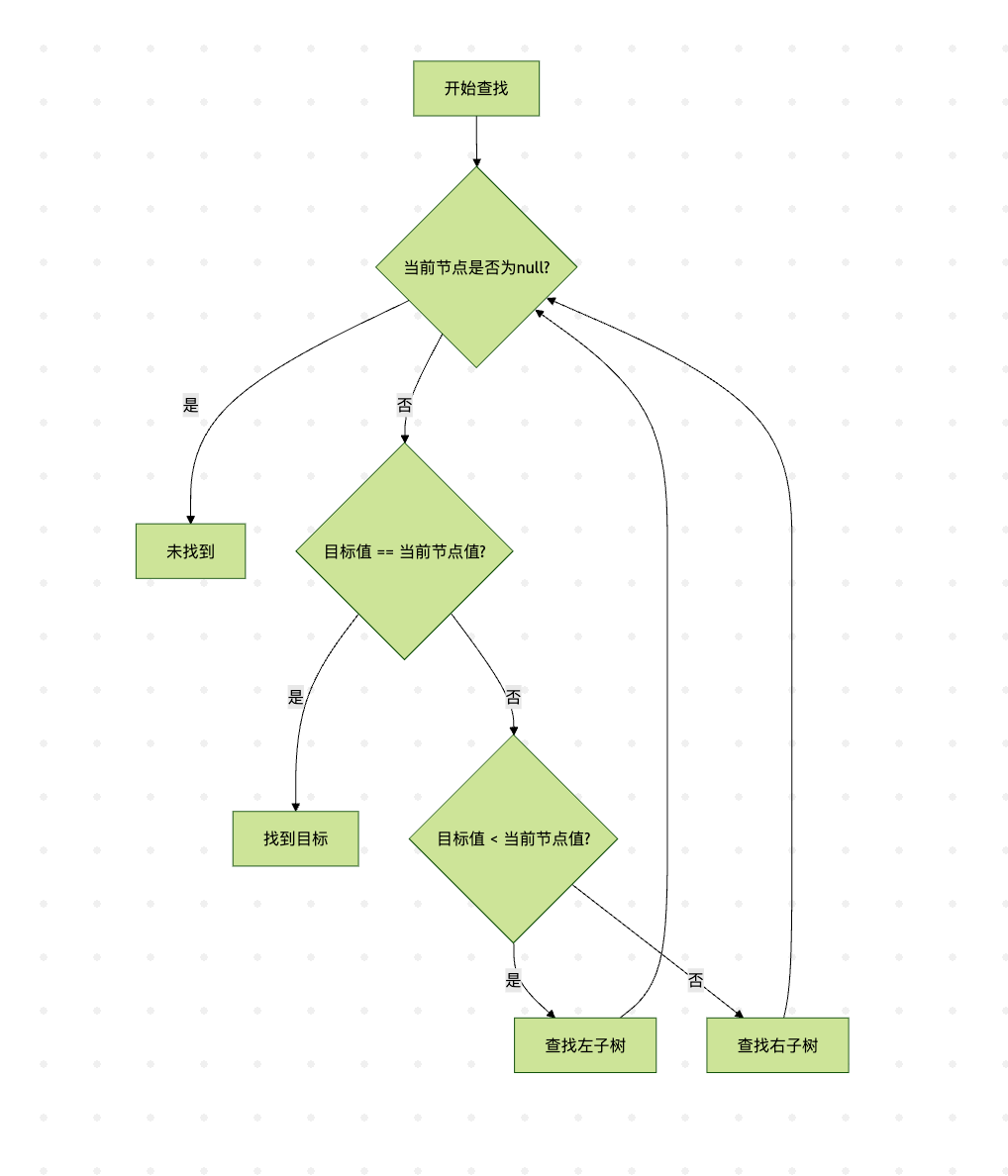
以上流程图说明了二叉搜索树的查找过程，它通过不断比较和选择子树来缩小搜索范围。

下面是查找操作的Python实现：

class Node:def __init__(self, key):self.left = Noneself.right = Noneself.val = keydef search(root, key):# 基本情况：根节点为空或键值等于根节点的键值if root is None or root.val == key:return root# 键值大于根节点的键值，则在右子树中查找if root.val < key:return search(root.right, key)# 键值小于根节点的键值，则在左子树中查找return search(root.left, key)

上述代码展示了二叉搜索树的递归查找实现。为了清晰展示查找过程，代码中包含了三种基本情况：找到目标、查找左子树和查找右子树。

2. 插入操作

理解了查找操作后，我们来看看如何向BST中插入新节点。插入操作的关键是找到合适的位置，保持BST的性质不被破坏。

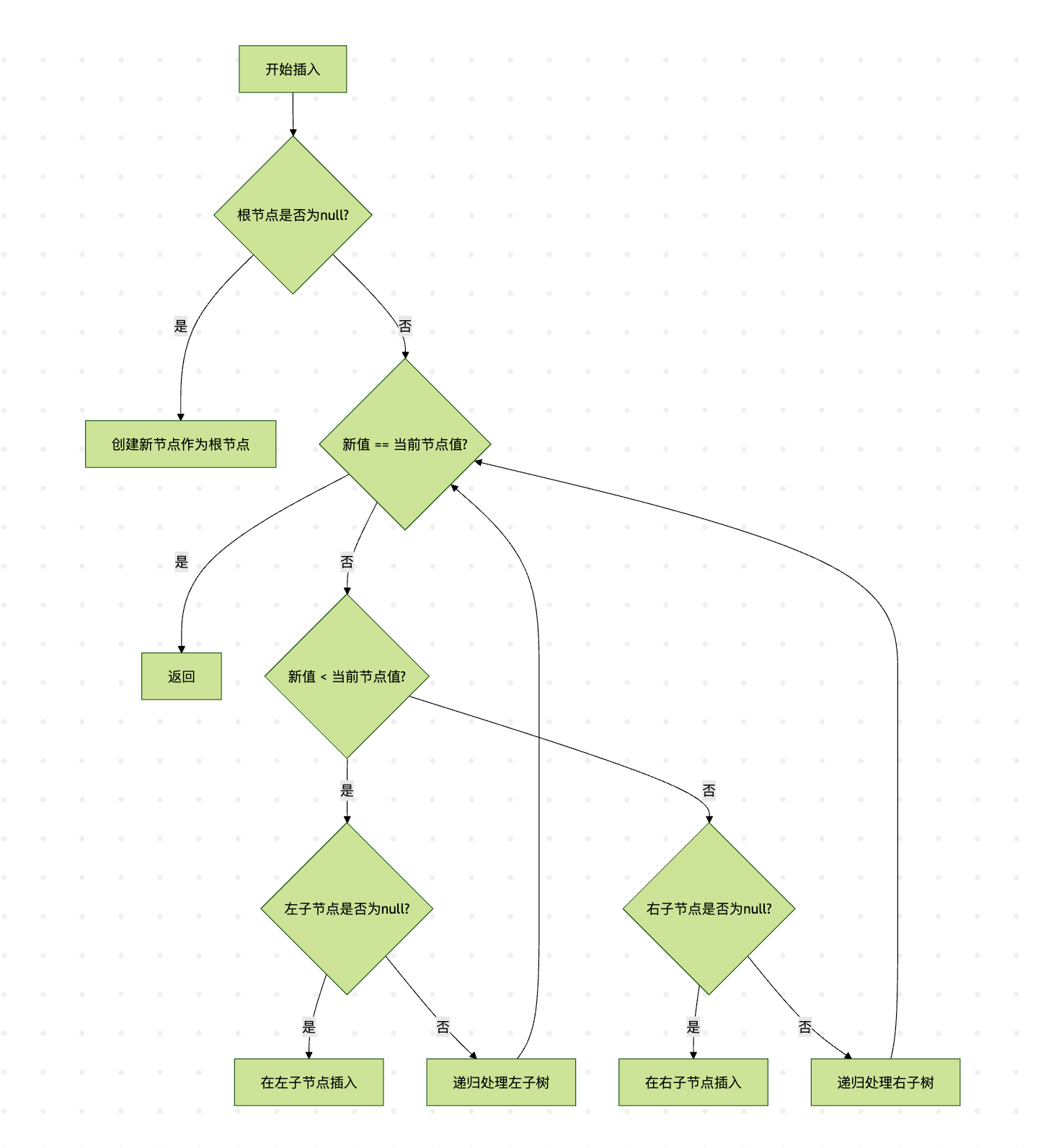
这个流程图展示了插入操作的完整过程，它需要找到合适的位置并保持BST的性质。

下面是插入操作的Python实现：

def insert(root, key):# 如果树为空，返回新节点if root is None:return Node(key)# 否则递归查找插入位置if key < root.val:root.left = insert(root.left, key)elif key > root.val:root.right = insert(root.right, key)# 返回(未修改的)节点指针return root

考虑到实际应用中可能需要处理重复值的情况，上述代码使用了elif结构来确保不插入重复值。这种递归实现方式简洁明了，能够很好地保持BST的性质。

3. 删除操作

删除操作是BST中最复杂的操作，因为它需要考虑三种不同的情况：

1. 要删除的节点是叶子节点（没有子节点）
2. 要删除的节点有一个子节点
3. 要删除的节点有两个子节点

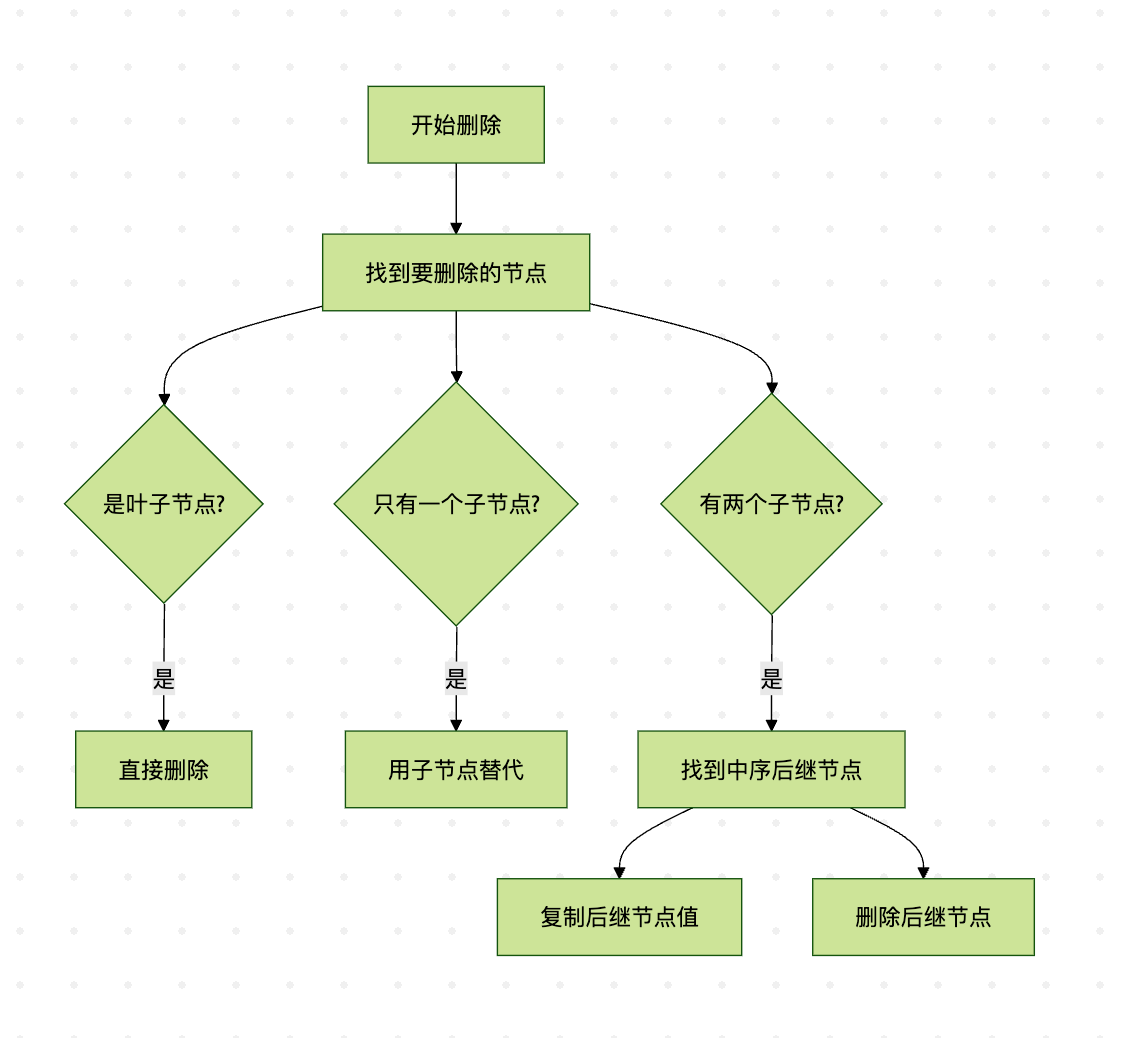
这个流程图清晰地展示了删除操作需要考虑的三种情况及其处理方式。

下面是删除操作的Python实现：

def deleteNode(root, key):# 基本情况：树为空if root is None:return root# 递归查找要删除的节点if key < root.val:root.left = deleteNode(root.left, key)elif key > root.val:root.right = deleteNode(root.right, key)else:# 节点只有一个子节点或没有子节点if root.left is None:return root.rightelif root.right is None:return root.left# 节点有两个子节点：获取中序后继（右子树的最小值）temp = minValueNode(root.right)# 复制中序后继的内容到当前节点root.val = temp.val# 删除中序后继root.right = deleteNode(root.right, temp.val)return rootdef minValueNode(node):current = nodewhile current.left is not None:current = current.leftreturn current

上述代码实现了BST的删除操作。为了处理有两个子节点的情况，代码中使用了辅助函数minValueNode来找到右子树的最小值节点（中序后继）。这种方案确保了在删除节点后，BST的性质仍然得以保持。

三、二叉搜索树的性能分析

通过前面的讨论，相信大家对BST的基本操作已经有了清晰的认识。现在我们来看看它的性能特点。

BST的性能高度依赖于树的形状：

• 最好情况：树完全平衡，高度为log₂n，所有操作都是O(log n)
• 最坏情况：树退化为链表，高度为n，所有操作都是O(n)

小贴士：在实际应用中，我们通常会使用平衡二叉搜索树（如AVL树、红黑树）来避免最坏情况的发生，保持较高的操作效率。

四、二叉搜索树的应用场景

通过前面的性能分析，我们知道了BST的优势和局限。那么在实际开发中，BST有哪些典型的应用场景呢？

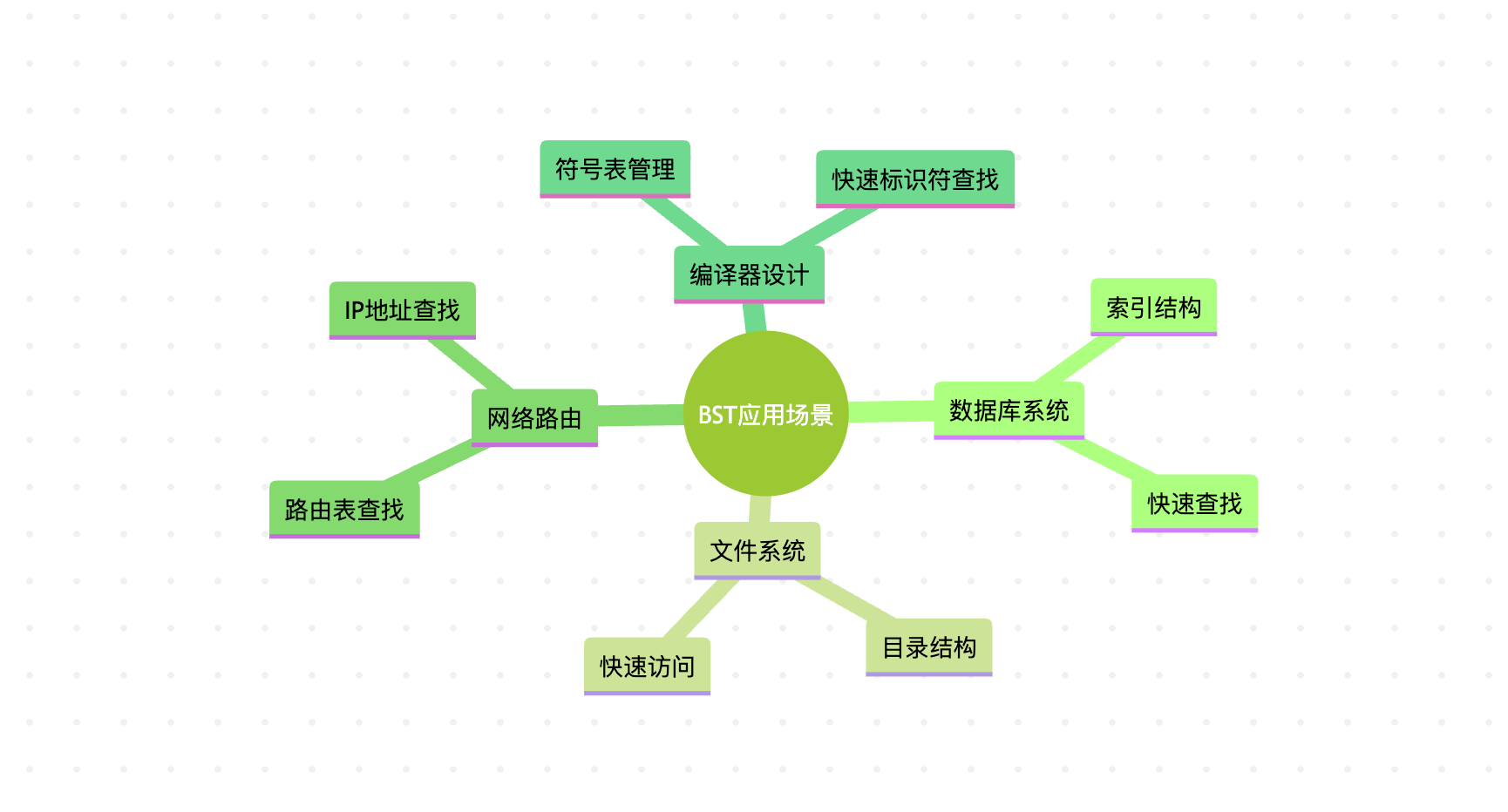
这个思维导图展示了二叉搜索树在不同领域的应用场景，它在需要高效查找的系统中发挥着重要作用。

具体来说：

1. 数据库索引：许多数据库系统使用BST或其变种（如B树、B+树）来实现索引，加速数据检索
2. 内存中的查找结构：当需要频繁查找且数据量适中时，BST是很好的选择
3. 排序：对BST进行中序遍历可以得到有序的数据序列
4. 范围查询：BST可以高效地找到某个范围内的所有值

注意：虽然BST有很多优点，但它并不适合所有场景。对于频繁插入删除且需要保持平衡的场景，建议考虑平衡二叉搜索树。

五、总结

通过今天的讨论，相信大家对二叉搜索树有了全面的认识。让我们回顾一下本文的主要内容：

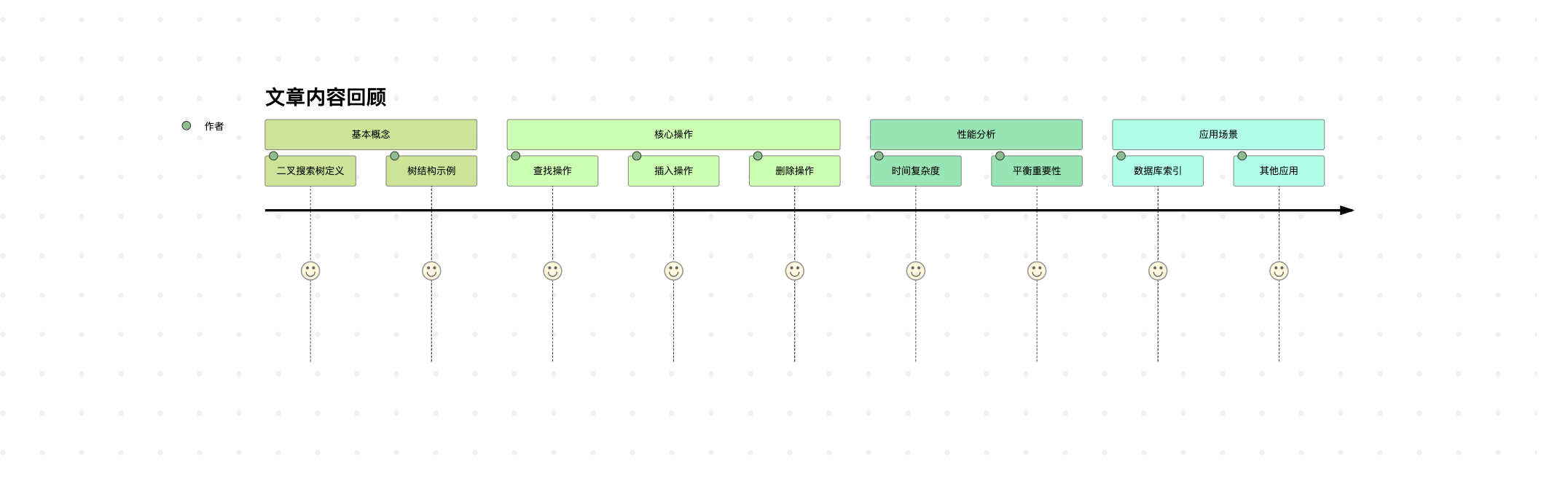
这个旅程图总结了本文的目录结构，从基本概念到实际应用，全面覆盖了二叉搜索树的知识点。

二叉搜索树作为一种基础而强大的数据结构，在计算机科学中占有重要地位。虽然它有一些局限性，但理解BST的工作原理对我们学习更复杂的树结构（如AVL树、红黑树、B树等）至关重要。

我建议大家在理解基本原理后，可以尝试自己实现一个BST，并测试它的各种操作。通过实践，你会对BST有更深刻的理解。

希望这篇文章能帮助大家掌握二叉搜索树的核心知识。如果你有任何问题或想法，欢迎随时交流讨论！