LeetCode热题100【第4天】

第一题 除自身以外的数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法，且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示：
2 <= nums.length <= 105
-30 <= nums[i] <= 30
输入 保证 数组 answer[i] 在 32 位 整数范围内
题解：

class Solution:def productExceptSelf(self, nums: List[int]) -> List[int]:res = [1] * len(nums)t = 1for i in range(len(nums)):res[i] *= tt *= nums[i]t = 1for i in range(len(nums) - 1, -1, -1):res[i] *= tt *= nums[i]return res

第二题 缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1：
输入：nums = [1,2,0]
输出：3
解释：范围 [1,2] 中的数字都在数组中。
示例 2：
输入：nums = [3,4,-1,1]
输出：2
解释：1 在数组中，但 2 没有。
示例 3：
输入：nums = [7,8,9,11,12]
输出：1
解释：最小的正数 1 没有出现。
提示：
1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
题解：

class Solution:def firstMissingPositive(self, nums: List[int]) -> int:set_nums = set(nums)t = 1while t in set_nums:t += 1return t

第三题 矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
示例 1：

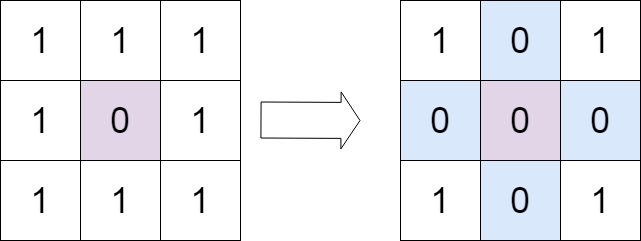
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]
示例 2：

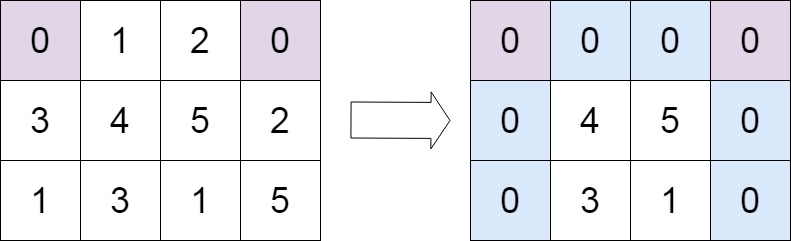
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示：
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1

class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""x = [0] * len(matrix)y = [0] * len(matrix[0])for i in range(len(matrix)):for j in range(len(matrix[i])):if matrix[i][j] == 0:x[i] = 1y[j] = 1for i in range(len(matrix)):if x[i] == 1:matrix[i][:] = [0] * len(matrix[i])continuefor j in range(len(matrix[i])):if y[j] == 1:matrix[i][j] = 0

第四题 螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。
示例 1：

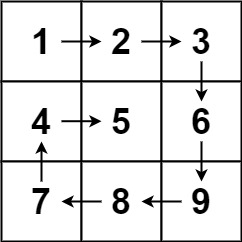
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]
示例 2：

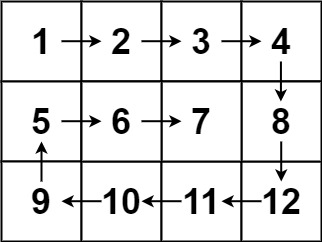
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]
提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100
题解：

class Solution:def spiralOrder(self, matrix: List[List[int]]) -> List[int]:n = len(matrix)m = len(matrix[0])visited = [[False] * (m) for _ in range(n)]turn = [[0, 1], [1, 0], [0, -1], [-1, 0]]t = 0i = 0j = 0res = []for _ in range(n * m - 1):res.append(matrix[i][j])visited[i][j] = Trueti, tj = i + turn[t][0], j + turn[t][1]while (ti < 0 or ti >= n) or (tj < 0 or tj >= m) or visited[ti][tj]:t = (t + 1) % 4ti, tj = i + turn[t][0], j + turn[t][1]i, j = ti, tjres.append(matrix[i][j])return res

第五题 旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1：

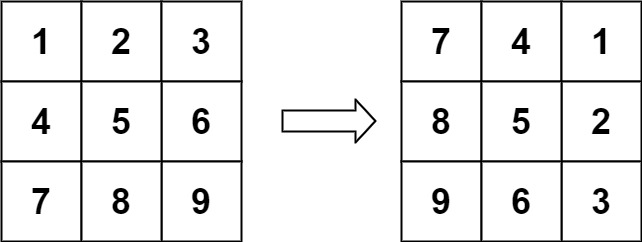
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]
示例 2：

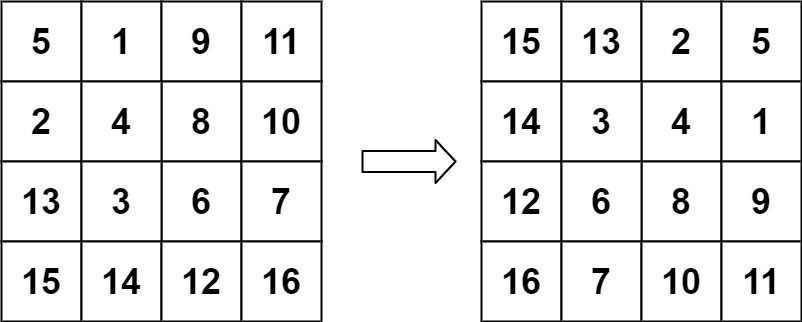
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示：
n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000
题解：

class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""n = len(matrix)for i in range(n // 2):for j in range((n + 1) // 2):t = matrix[i][j]matrix[i][j] = matrix[n - j - 1][i]matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]matrix[j][n - i - 1] = t