【算法训练营Day14】二叉树part4

找树左下角的值

题目链接：513. 找树左下角的值

解题逻辑：

使用层序遍历，将最后一层的第一个元素拿出来即可。

class Solution {public int findBottomLeftValue(TreeNode root) {Deque<List<Integer>> allItem = new LinkedList<>();Deque<TreeNode> que = new ArrayDeque<>();que.add(root);while(!que.isEmpty()) {List<Integer> row = new ArrayList<>();int count = que.size();while(count > 0) {TreeNode node = que.remove();count--;row.add(node.val);if(node.left != null) que.add(node.left);if(node.right != null) que.add(node.right);}allItem.add(row);}return allItem.removeLast().get(0);}
}

路径总和

题目链接：112. 路径总和

解题逻辑：

这个题可以当作257. 二叉树的所有路径这道题的延深，我们可以沿用此题的代码，最后遍历每条路径上的和是否有符合条件的即可。

class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if(root == null) return false;Deque<Integer> path = new ArrayDeque<>();List<Integer> allPathsAdd = new ArrayList<>();getAllPath(root,path,allPathsAdd);for(Integer sum : allPathsAdd) if(targetSum == sum) return true;return false;}public void getAllPath(TreeNode node,Deque<Integer> path,List<Integer> allPathsAdd){path.add(node.val);if(node.left == null && node.right == null) {int add =  0;for(Integer num : path) add += num;allPathsAdd.add(add);}if(node.left != null) {getAllPath(node.left,path,allPathsAdd);path.removeLast();}if(node.right != null) {getAllPath(node.right,path,allPathsAdd);path.removeLast();}}
}

上面的代码是在257代码的基础上修改而来，这样其实效率并不是很高，因为我们相当于是把所有路径遍历了出来，然后再检验是否存在符合条件的路径，但其实我们在遍历的途中发现有一条路径已经符合条件了，那么就可以直接返回了，这样就大大提升了效率。

修改后的代码如下：

class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if(root == null) return false;int count = 0;return getPathSum(root,count,targetSum);}public boolean getPathSum(TreeNode node,int count,int targetSum){count += node.val;if(node.left == null && node.right == null) {if(count == targetSum) return true;return false;}if(node.left != null) {boolean left = getPathSum(node.left,count,targetSum);if(left == true) return true;}if(node.right != null) {boolean right = getPathSum(node.right,count,targetSum);if(right == true) return true;}return false;}
}

总结：递归函数的返回值

递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：

• 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的113.路径总和ii）
• 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍）
• 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）

路径总和 II

题目链接：113. 路径总和 II

与上一题的区别在于，本题要寻找所有符合条件的路径，所以要遍历整棵树，并且我们对递归的返回值也不做处理，所以我们的递归方法可以不设置返回值。

代码如下：

class Solution {public List<List<Integer>> pathSum(TreeNode root, int targetSum) {if(root == null) return new ArrayList<List<Integer>>();List<Integer> path = new ArrayList<>();List<List<Integer>> result = new ArrayList<>();getPathSum(root,path,targetSum,result);return result;}public void getPathSum(TreeNode node,List<Integer> path,int targetSum,List<List<Integer>> result){path.add(node.val);if(node.left == null && node.right == null) {int count = 0;for(Integer num : path) count += num;if(count == targetSum) {List<Integer> deepCopy = new ArrayList<>();for (Integer obj : path) {deepCopy.add(obj); }result.add(deepCopy);   } return;}if(node.left != null) {getPathSum(node.left,path,targetSum,result);path.remove(path.size() - 1);}if(node.right != null) {getPathSum(node.right,path,targetSum,result);path.remove(path.size() - 1);}}
}

总结：二叉树递归的思考

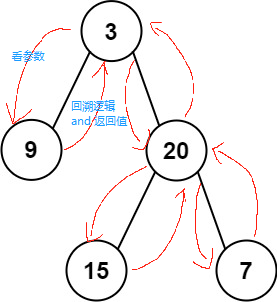
遍历的选择：看中的逻辑中需不需要左右的参与

递归，是递和归的两个过程：

• 参数是在递的过程中层层深入
• 返回值是在归的过程中逐层向上返回
• 而回溯算法的逻辑就在归的过程之后

从中序与后序遍历序列构造二叉树

题目链接：106. 从中序与后序遍历序列构造二叉树

解题逻辑：

首先要了解想要恢复一颗二叉树，那么一定需要两种遍历方法，其中中序遍历是一定需要的，而另一种遍历方式可以是前序、后序、层序遍历方式。

复原的原理如下图所示：

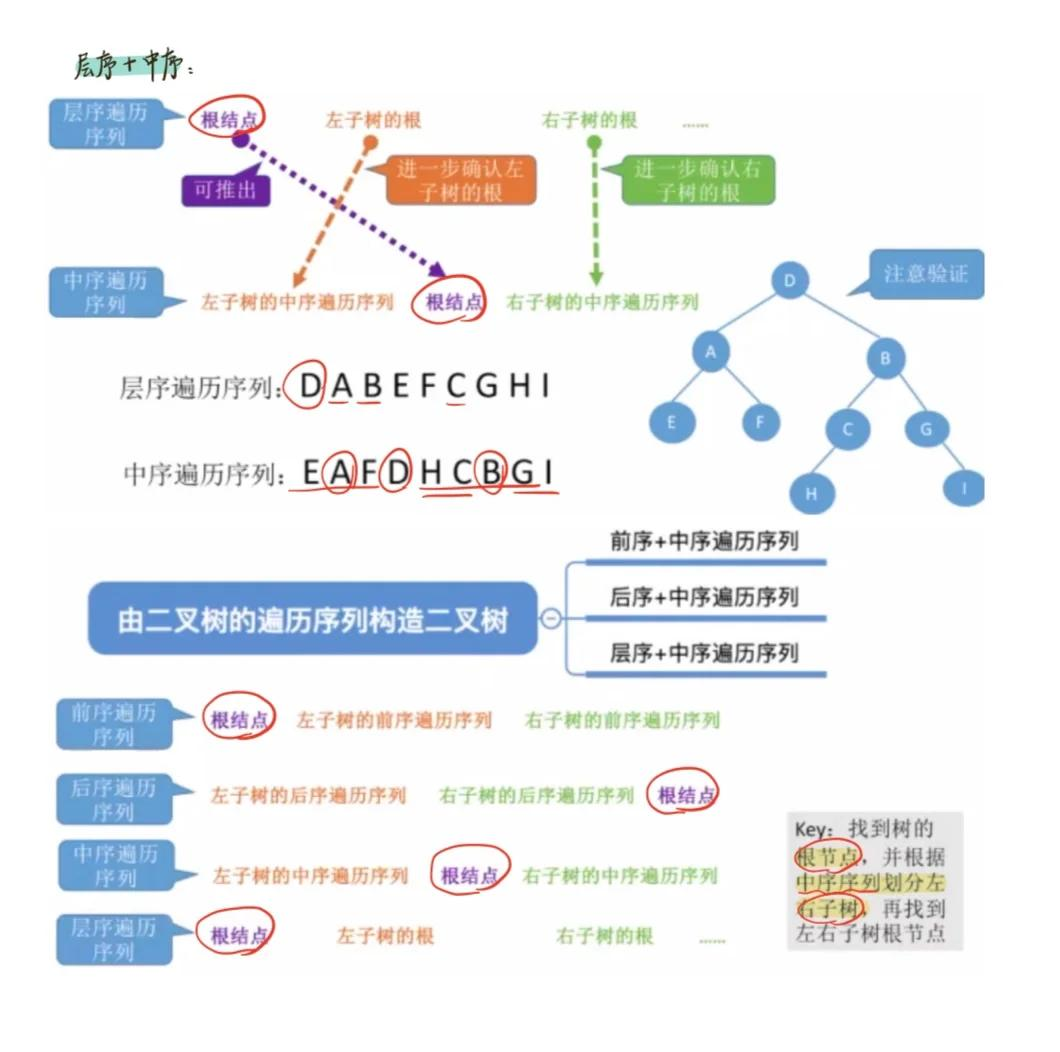
本题是考察通过中序和后序构造二叉树，其中后序遍历是用来确定根节点的，而中序是用来确定根节点的左右子树情况的。

本题选用后序遍历的递归方式，这样最后可以将左右子树的根节点拼接到二叉树的根节点左右。接下来从递归三部曲开始分析：

• 递归的参数与返回值：返回值为TreeNode，而参数为前序列表与后序列表，接下来将会对他递归切割
• 递归出口：当后序列表长度为0的时候，直接返回null。当后序列表的长度为1的时候，则直接根据这个值构建节点返回
• 递归单层逻辑：
  • 取到后序列表的最后一个元素，作为当前递归根节点
  • 在中序列表中找到该元素
  • 根据该元素对中序列表、后序列表进行切割
  • 左递归获得左子节点
  • 右递归获得右子节点
  • 将左右子节点组装到根节点上
  • 返回根节点

代码如下：

class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {if(postorder.length == 0) return null;if(postorder.length == 1) return new TreeNode(postorder[0]);int devideNum = postorder[postorder.length - 1];TreeNode root = new TreeNode(devideNum);int[] inorderLeft = Arrays.copyOfRange(inorder, 0, findNum(inorder,devideNum));int[] postorderLeft = Arrays.copyOfRange(postorder, 0, inorderLeft.length);root.left = buildTree(inorderLeft,postorderLeft);int[] inorderRight;if(findNum(inorder,devideNum) == inorder.length - 1) {inorderRight = new int[0];}else {inorderRight = Arrays.copyOfRange(inorder, findNum(inorder,devideNum) + 1,inorder.length);}int[] postorderRight = Arrays.copyOfRange(postorder, postorderLeft.length, postorder.length - 1);root.right = buildTree(inorderRight,postorderRight);return root;}public int findNum(int[] nums,int target){for(int i = 0;i < nums.length;i++) {if(nums[i] == target) return i;}return -1;}
}