C++ RB_Tree
一、红黑树是什么?—— 带颜色标记的平衡二叉搜索树
红黑树是一种自平衡二叉搜索树,它在每个节点上增加了一个颜色属性(红色或黑色),通过对颜色的约束来确保树的大致平衡。这种平衡策略被称为 "弱平衡",相较于严格平衡的 AVL 树,它允许节点间的高度差不超过两倍,从而减少了旋转操作的频率,提升了动态数据操作的效率。
核心特性:
- 二叉搜索树属性:左子树所有节点值小于根节点,右子树所有节点值大于根节点
- 颜色标记机制:每个节点非红即黑,通过颜色调整维持平衡
- 近似平衡:任何节点到其后代叶子节点的最长路径,不超过最短路径的 2 倍
二、红黑树的三大核心优势
1. 稳定的对数时间复杂度
- 查找 / 插入 / 删除均保持 O (log n) 的时间复杂度,优于普通 BST 的 O (n) 最坏情况
- 对比 AVL 树:虽然 AVL 树高度平衡(高度差≤1),但红黑树在频繁插入删除场景下,旋转次数更少,实际性能更优
2. 高效的动态数据操作
- 插入和删除时仅需最多 2 次旋转(AVL 树可能需要 4 次)
- 颜色重涂操作复杂度远低于树结构调整,适合处理频繁变更的数据集合
3. 广泛的实际应用
- Java 集合框架:TreeMap 和 TreeSet 的底层实现
- C++ STL:map、multimap 内部采用红黑树
- Linux 内核:用于管理内存区域(vm_area_struct)
- Nginx:实现对客户端请求的高效管理
三、红黑树的五条核心规则(必须严格遵守)
规则 1:节点颜色二值化
每个节点只能是红色或黑色,这是整个约束体系的基础。
规则 2:根节点恒定为黑色
确保树的最顶层始终为黑色,避免出现根节点为红色带来的平衡隐患。
规则 3:叶子节点全为黑色
这里的叶子节点指的是 NIL 空节点(外部节点),所有真实节点的叶子都指向这些黑色哨兵节点。
规则 4:红色节点必有黑色子节点
任何红色节点的左右子节点必须为黑色,防止出现 "红 - 红" 相邻的情况,这是维持平衡的关键约束。
规则 5:黑色高度统一
从任一节点到其所有后代叶子节点的路径上,包含的黑色节点数量必须相同。这个 "黑色高度" 的一致性,保证了树的最长路径不超过最短路径的 2 倍(因为红色节点不能连续出现,最长路径 = 黑色高度 + 红色节点数,而红色节点数≤黑色高度)。

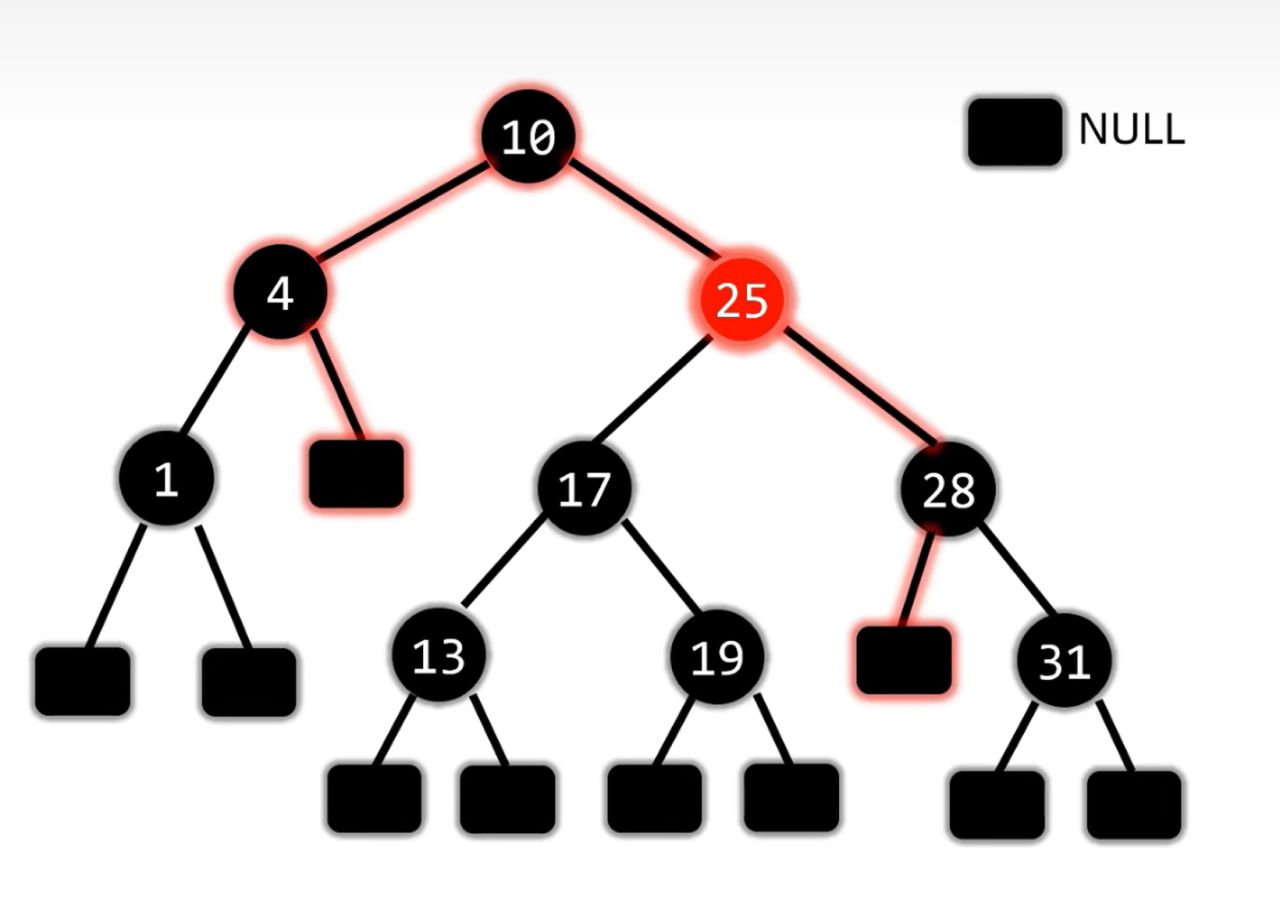
比如我们看这课树

看起来好像是红黑树!!!
但是实际上我们把NULL节点画出来会发现每条路径上的黑色节点个数并不相同
所以它不是一棵二叉树
根据红黑树的五条性质可以保证
红黑树最长路径长度(节点数)不超过最短路径长度的 2 倍(含NULL节点)
四、红黑树的平衡维护机制
当插入或删除节点导致颜色规则被破坏时,通过两种操作恢复平衡:
- 颜色重涂:改变节点颜色(红→黑或黑→红)
- 树旋转:分为左旋和右旋,调整树结构
- 下面以图的形成呈现
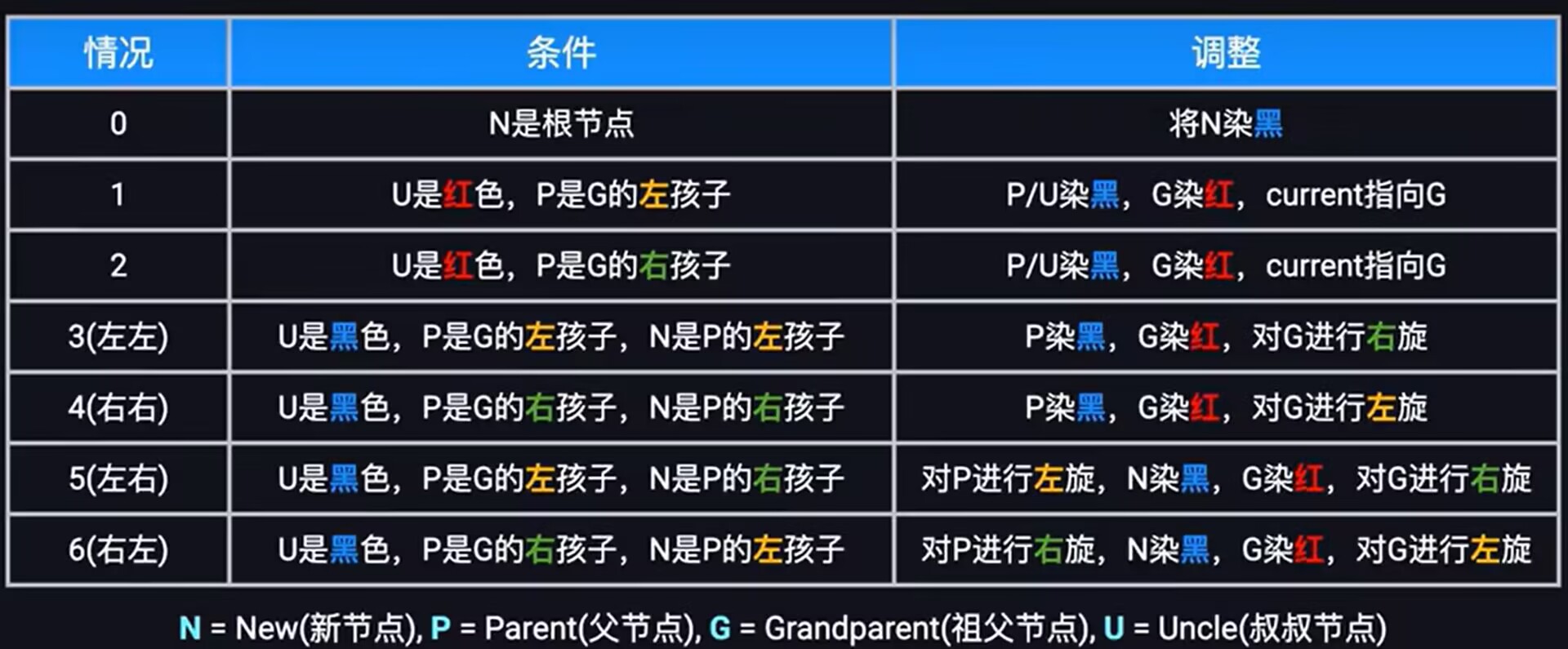





注意以下错误示范

