当前位置： 首页 > news >正文

摩尔条纹 原理以及matlab 实现

news 来源：原创 2025/5/31 3:02:18

一、简介

莫尔条纹的形成原理-CSDN博客

“莫尔”一词源于法文“Moire”，其原本的含义是“波动”或者“起波纹的”。早在古代时期，人们便偶然发现，当把两块薄的丝绸织物相互叠加放置时，能够看到一种呈现不规则形态的花纹。此后，人们就把由两种条纹相互叠加而产生的图形命名为莫尔条纹。

在1874年的时候，英国著名的物理学家瑞利率先将莫尔条纹当作一种计量测试的手段，由此开创了莫尔测试技术这一崭新的领域。

从广义的范畴来讲，莫尔测试技术理应涵盖所有把莫尔图案作为计量测试手段的各类方法。不过，按照习惯上的说法，它通常是特指利用计量光栅元件来产生莫尔条纹的那一类计量测试方法，也就是我们常说的光栅莫尔条纹法。

时至今日，莫尔条纹已经在科学研究以及工程技术等诸多领域得到了极为广泛的应用。作为一种精密的计量手段，莫尔条纹可应用于测角、测长、测振等不同的专业领域当中。并且，随着光电子技术不断向前发展，莫尔条纹在自动跟踪、轨迹控制、变形测试以及三维物体表面轮廓测试等方面，同样有着十分广泛的应用。

简单的说就是：

莫尔条纹（Moire Pattern）是一种由两个周期性图案重叠时产生的干涉现象，表现为明暗相间的条纹。其原理基于光的干涉和周期结构的相互作用。

 

原本静止的条纹在移动另一个条纹的时候整个都动起来了 

莫尔条纹是什么？当栅格纸经过“图案”时，有趣的科学现象发生了_哔哩哔哩_bilibili

二、分类

 针对莫尔条纹的形成原理，已经发展出了多种理论，大致可归纳为以下三种：

一，基于遮光原理来阐释。该理论主张莫尔条纹的产生，是源于一块光栅的不透光线纹对另一块光栅透光缝隙产生的遮挡作用。所以，能够依据光栅副叠合线纹的交点轨迹，去呈现亮条纹的亮度分布情况。
二，基于衍射干涉原理来解释。按照这一理论，由条纹所构建形成的全新亮度分布，可以通过衍射波之间相互干涉所产生的结果来加以描述。


三，基于傅里叶变换原理来解释。依据傅里叶变换原理，能够把光栅副透射光场分解成为具有不同空间频率的离散分量，而莫尔条纹恰恰是由那些低于光栅频率的空间频率项所构成的。
 

三、遮光原理

遮光原理

当两个具有相似周期或旋转角度的图案（如光栅、网格、线条等）重叠时，它们的透光或反射部分会相互调制，产生低频的、肉眼可见的条纹（莫尔条纹）。这个光栅结构可以是实际光栅，也可以是光栅的像。由于两块光栅的栅距相等（或近似相等），并且线纹宽度等于线纹间距，线纹间又有微小的夹角，那么两块光栅的线纹必然在空间相交。透过光线的区域形成亮带，不透光的区域形成暗带，其余区域介于亮带与暗带之间，这样就构成了清晰的莫尔条纹图像。

最常用的方法：

几何法

直观、简便只适用于局部；

序数方程法

适用于全场，可导出莫尔条纹方程。

方法1：叠加两个正弦波栅格

% 设置参数
width = 500; % 图像宽度
height = 500; % 图像高度
f1 = 0.05; % 第一个栅格的频率
f2 = 0.04; % 第二个栅格的频率
theta = 10; % 第二个栅格的旋转角度(度)% 创建网格
[x, y] = meshgrid(1:width, 1:height);% 生成第一个正弦波栅格(水平方向)
pattern1 = sin(2*pi*f1*x);
imshow(pattern1, []);
title('正弦波栅格条纹1')% 生成第二个正弦波栅格(旋转一定角度)
x_rot = x*cosd(theta) + y*sind(theta);
pattern2 = sin(2*pi*f2*x_rot);
imshow(pattern2, []);
title('正弦波栅格条纹2')% 叠加两个图案生成摩尔条纹
moire = pattern1 + pattern2;imshow(pattern1, []);
imshow(pattern2, []);% 显示结果
figure;
imshow(moire, []);
title('正弦波栅格生成的摩尔条纹');
colormap(gray);

正弦波1

正弦波2

合成的摩尔波纹

 方法2：叠加两个圆形栅格

% 设置参数
width = 500;
height = 500;
f1 = 0.03; % 第一个圆形栅格的频率
f2 = 0.025; % 第二个圆形栅格的频率
cx = width/2; % 中心x坐标
cy = height/2; % 中心y坐标% 创建网格
[x, y] = meshgrid(1:width, 1:height);% 计算到中心的距离
r = sqrt((x-cx).^2 + (y-cy).^2);% 生成两个圆形栅格
pattern1 = sin(2*pi*f1*r);pattern2 = sin(2*pi*f2*r);
imshow(pattern2, []);
title('圆形栅格生成的条纹2')% 叠加生成摩尔条纹
moire = pattern1 + pattern2;% 显示结果
figure;
imshow(moire, []);
title('圆形栅格生成的摩尔条纹');
colormap(gray);

圆形波1

圆形波2 

圆形摩尔纹 

方法3：叠加两个不同角度的直线栅格

合成条纹：

 

% 参数设置
N = 512; % 图像大小
d1 = 20; % 光栅1周期（像素）
d2 = 22; % 光栅2周期（像素）
theta = 5; % 光栅2旋转角度（度）% 生成光栅1（水平方向）
[x, y] = meshgrid(1:N, 1:N);
grating1 = 0.5 + 0.5 * cos(2*pi*x/d1);% 生成光栅2（旋转theta角度）
theta_rad = deg2rad(theta);
x_rot = x*cos(theta_rad) + y*sin(theta_rad);
grating2 = 0.5 + 0.5 * cos(2*pi*x_rot/d2);% 叠加光栅生成摩尔条纹
moire_pattern = grating1 .* grating2;% 显示结果
figure;
subplot(1,3,1); imshow(grating1, []); title('光栅1');
subplot(1,3,2); imshow(grating2, []); title('光栅2');
subplot(1,3,3); imshow(moire_pattern, []); title('摩尔条纹');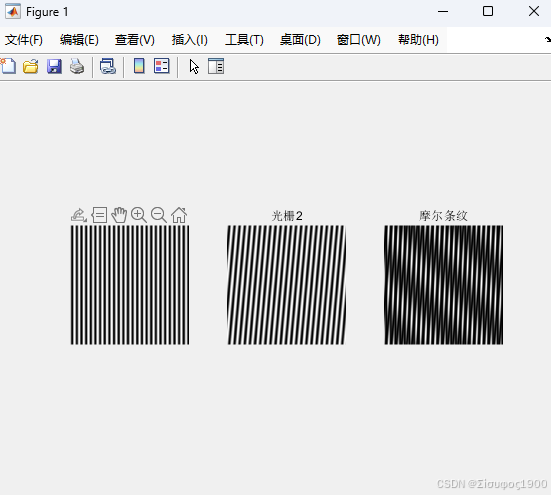

总结：

四、衍射干涉原理

方法一：双光束干涉

  1. 装置：分束器将激光分为两束相干光，以微小角度 θ交汇。

  2. 干涉：两束光在重叠区域形成等间距干涉条纹（类似杨氏双缝），条纹间距 Δx 为：

    其中 λ 为光波长。

  3. 摩尔条纹：若干涉光栅与另一光栅叠加，会形成次级摩尔条纹。

% 参数设置
N = 512; % 图像大小
lambda = 10; % 波长（像素）
theta = 0.1; % 两光束夹角（弧度）% 生成干涉条纹
[x, y] = meshgrid(1:N, 1:N);  % 生成512*512 的图像
beam1 = exp(1i * 2*pi * sin(theta/2) * x / lambda);
beam2 = exp(1i * 2*pi * sin(-theta/2) * x / lambda);
interference = abs(beam1 + beam2).^2;% 显示结果
figure;
imshow(interference, []);
title('双光束干涉条纹');
colorbar;

方法二：Talbot 自成像效应

  1. 单光栅衍射：一束平行光通过周期性光栅后，在特定距离会自成像。

  2. 叠加第二光栅：在 Talbot 距离附近放置第二光栅，与自成像光栅叠加产生摩尔条纹。

% 参数设置
N = 512; % 图像大小
d = 20; % 光栅周期（像素）
lambda = 632.8e-9; % 波长（m）
z_T = 2 * d^2 / lambda; % Talbot 距离（理论计算）% 生成初始光栅（正弦光栅）
[x, y] = meshgrid(1:N, 1:N);
grating = 0.5 + 0.5 * cos(2*pi*x/d);% 模拟光传播（菲涅尔衍射）
k = 2*pi/lambda;
z = z_T / 10; % 观察距离（小于Talbot距离）
propagated = fft2(grating);
[fx, fy] = meshgrid((-N/2:N/2-1)/N, (-N/2:N/2-1)/N);
H = exp(1i * k * z * sqrt(1 - (lambda*fx).^2 - (lambda*fy).^2));
propagated = ifft2(propagated .* fftshift(H));% 叠加第二光栅生成摩尔条纹
grating2 = 0.5 + 0.5 * cos(2*pi*x/(d+2)); % 周期略有不同
moire_talbot = abs(propagated) .* grating2;% 显示结果
figure;
subplot(1,3,1); imshow(grating, []); title('初始光栅');
subplot(1,3,2); imshow(abs(propagated), []); title('衍射后光场');
subplot(1,3,3); imshow(moire_talbot, []); title('Talbot 摩尔条纹');

五、傅里叶变换原理

 方法1：频域合成两光栅的叠加

步骤：

其核心思想是通过频域操作（如滤波、频谱叠加）控制空域周期性结构的叠加效果

  1. 在频域生成两个不同频率的正弦光栅频谱。

  2. 通过傅里叶逆变换（IFFT）得到空域光栅。

  3. 叠加两光栅生成摩尔条纹。

% 参数设置
N = 512;                % 图像大小
f1 = 1/20;              % 光栅1的频率（周期=20像素）
f2 = 1/22;              % 光栅2的频率（周期=22像素）% 生成频域坐标
[fx, fy] = meshgrid(-N/2:N/2-1);
fx = fx / N; fy = fy / N;% 生成两个光栅的频谱（狄拉克函数模拟理想光栅）
G1 = zeros(N);
G1(abs(fx - f1) < 0.001 & abs(fy) < 0.001) = 1;  % 光栅1（沿x方向）
G2 = zeros(N);
G2(abs(fx - f2) < 0.001 & abs(fy) < 0.001) = 1;  % 光栅2（沿x方向）% 傅里叶逆变换得到空域光栅
grating1 = real(ifft2(ifftshift(G1)));
grating2 = real(ifft2(ifftshift(G2)));% 叠加光栅生成摩尔条纹
moire_pattern = grating1 .* grating2;% 显示结果
figure;
subplot(1,3,1); imshow(grating1, []); title('光栅1 (频域生成)');
subplot(1,3,2); imshow(grating2, []); title('光栅2 (频域生成)');
subplot(1,3,3); imshow(moire_pattern, []); title('摩尔条纹');

 方法2：频域直接构造摩尔条纹频谱

  1. 摩尔条纹的频谱是两光栅频谱的卷积。

  2. 直接在频域构造卷积后的频谱，再逆变换得到空域条纹。

% 参数设置
N = 512;
f1 = 1/20;      % 光栅1频率
f2 = 1/22;      % 光栅2频率% 生成频域坐标
[fx, fy] = meshgrid(-N/2:N/2-1);
fx = fx / N;% 构造两光栅频谱的卷积（摩尔条纹频谱）
moire_spectrum = zeros(N);
moire_spectrum(abs(fx - (f1 - f2)) < 0.001) = 1;  % 低频摩尔条纹成分% 傅里叶逆变换得到空域摩尔条纹
moire_pattern = real(ifft2(ifftshift(moire_spectrum)));% 显示结果
figure;
subplot(1,2,1); imshow(log(abs(fftshift(moire_spectrum)) + 1), []); title('摩尔条纹频谱');
subplot(1,2,2); imshow(moire_pattern, []); title('空域摩尔条纹');

 

 方法3：通过频域滤波增强摩尔条纹

  1. 对两光栅叠加后的图像进行傅里叶变换。

  2. 在频域滤除高频成分，保留低频摩尔条纹。

  3. 逆变换后得到纯净的摩尔条纹。

% 生成两光栅叠加的空域图像（同方法1）
[x, y] = meshgrid(1:N);
grating1 = cos(2*pi*f1*x);
grating2 = cos(2*pi*f2*x);
moire_raw = grating1 .* grating2;% 傅里叶变换
moire_fft = fftshift(fft2(moire_raw));% 设计低通滤波器（保留低频摩尔条纹）
cutoff = 0.02;  % 截止频率
H = sqrt(fx.^2 + fy.^2) < cutoff;% 频域滤波
filtered_spectrum = moire_fft .* H;% 逆变换得到滤波后的摩尔条纹
moire_filtered = real(ifft2(ifftshift(filtered_spectrum)));% 显示结果
figure;
subplot(1,3,1); imshow(moire_raw, []); title('原始叠加光栅');
subplot(1,3,2); imshow(log(abs(moire_fft) + 1), []); title('原始频谱');
subplot(1,3,3); imshow(moire_filtered, []); title('滤波后摩尔条纹');

关键参数说明

参数作用
f1, f2控制两光栅的频率，差异越小，摩尔条纹周期越大。
cutoff低通滤波的截止频率，影响摩尔条纹的清晰度。
N图像分辨率，值越大模拟越精细，但计算量增加。

 六、应用场景

  • 精密测量：用于检测微小位移、形变或振动（如光栅尺）。

  • 防伪技术：纸币、证件上的莫尔图案用于防伪。

  • 图像处理：消除扫描图像时的摩尔纹（如去摩尔纹滤镜）。

  • 艺术设计：通过叠加图案创造动态视觉效果。

相关文章：

  • 一站式掌握视频编辑器开发：OpenCV + Qt + FFmpeg 实战课程全览
  • 如何区分防爆手机与普通手机？
  • FFMPEG推流器讲解
  • # 使用 Selenium 爬取苏宁易购优质评价
  • 面试加分秘籍：校招数据倾斜场景下的SQL优化方案
  • AI 产品的 MVP 构建逻辑：Prompt 工程 ≠ 产品工程？
  • LabVIEW 中内存释放相关问题
  • LiveQing 视频点播流媒体 RTMP 推流服务功能：搭建 RTMP 视频流媒体服务详细指南
  • 2025年软件测试面试八股文（含答案+文档）
  • ORB-SLAM2学习笔记：ExtractorNode::DivideNode和ORBextractor::DistributeOctTree函数详解
  • 深度学习论文: FastVLM: Efficient Vision Encoding for Vision Language Models
  • 针对Python开发的工具推荐及分析，涵盖集成开发环境（IDE）、轻量级工具、在线开发平台、代码管理工具等）
  • 阅读笔记——理解什么是LLM大语言模型
  • 服务器带宽线路的区别（GIA、CN2、BGP、CMI等）
  • 技术为器，服务为本：AI时代的客服价值重构
  • 我在 Linux 进程管理中踩过的坑：僵尸、瞬时与不可中断进程实战实录
  • ffmpeg命令（二）：分解与复用命令
  • 杆塔倾斜在线监测装置：电力设施安全运行的“数字守卫”
  • 工商业储能的“智慧大脑”：解密 Acrel-2000ES EMS 的核心功能与价值
  • GB/T 36140-2018 装配式玻纤增强无机材料复合保温墙体检测
  • 公司外贸网站建设/杭州seo招聘
  • 17网站一起做网店白沟/软文广告是什么意思
  • 建站之星至尊版/2022最新热点事件及点评
  • 网站建设及经营应解决好的问题/seo技巧
  • 广州网站建设开发公司/双11销量数据
  • 如何做网站超链接/国外b站推广网站